本文目录导读:
除数与被除数的定义与理解
在数学的世界里,除法和它的相关概念是构成数学运算体系的重要基石,除数和被除数是除法运算中的两个核心概念,本文将详细探讨什么是除数,什么是被除数,以及它们在数学运算中的意义和应用。
除数的定义与理解
除数,在除法运算中,是执行“除”这一动作的对象,它表示将某个数(即被除数)按照指定的次数进行均分,在符号表示上,除数通常位于除号“÷”或分数线的右侧,在算式“10 ÷ 2”中,2就是除数,它表示将10均分为2份。
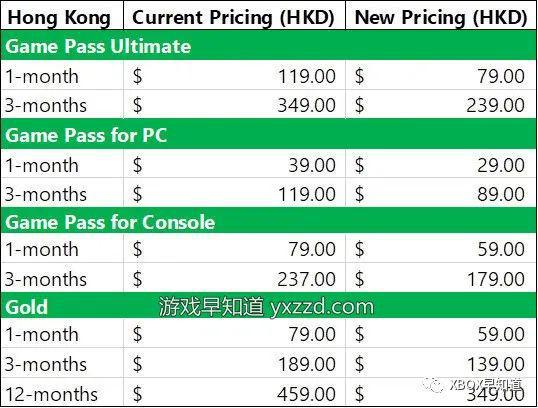
从数学本质上讲,除数是一个非零的数,因为任何数除以0在数学上都是没有定义的,除数可以是正数、负数、整数、分数或小数,在实际应用中,除数常常用来表示一个集合中的元素数量、一个过程的重复次数、或者一个数值的缩放比例等。
被除数的定义与理解
被除数,在除法运算中,是接受“除”这一动作的对象,它表示需要被均分的那个数,在符号表示上,被除数通常位于除号“÷”或分数线的左侧,在算式“10 ÷ 2”中,10就是被除数,它表示有10个单位需要被均分。
被除数同样可以是正数、负数、整数、分数或小数,在数学运算中,被除数的大小和性质决定了除法运算的结果,当被除数为正数时,若除数也为正数,则商为正;若除数为负数,则商为负,当被除数为负数时,情况则相反。

除数与被除数的关系与应用
除数和被除数在除法运算中相互依存,共同决定了运算的结果,它们之间的关系可以用一个简单的等式来表示:被除数 = 除数 × 商 + 余数,这个等式揭示了除法运算的本质,即被除数是由除数、商和余数共同构成的。
在实际应用中,除数和被除数的概念广泛应用于各个领域,在日常生活中,我们经常使用除法来计算平均值、比例、折扣等,在购物时,我们可能会用总价除以商品数量来计算每件商品的单价;在分配任务时,我们可能会用总任务量除以人数来计算每人需要完成的任务量。
在科学研究和工程技术中,除数和被除数的概念同样发挥着重要作用,在物理学中,我们经常使用除法来计算速度、加速度、密度等物理量;在经济学中,我们可能会用总产值除以总人数来计算人均产值;在计算机科学中,我们可能会用除法来进行数据归一化、比例缩放等操作。

除数和被除数是除法运算中的两个核心概念,除数表示执行“除”这一动作的对象,而被除数表示接受“除”这一动作的对象,它们在数学运算中相互依存,共同决定了运算的结果,通过深入理解除数和被除数的定义与关系,我们可以更好地掌握除法运算的本质和应用方法,为数学学习和实际应用打下坚实的基础。








发表评论