本文目录导读:
RSD:揭示数据精密度的关键指标
在科学研究和数据分析的广阔领域中,我们经常会遇到各种统计指标和术语,RSD(Relative Standard Deviation,相对标准偏差)是一个至关重要的概念,它为我们提供了一种量化数据离散程度、评估测量精密度的方法,本文将详细探讨RSD的定义、计算方法、应用场景以及其在数据分析中的重要作用。
RSD的定义
RSD,即相对标准偏差,是一个数学名词,用于描述数据集中各数值相对于其平均值的离散程度,RSD是标准偏差(Standard Deviation,SD)与数据平均值(Mean)的比值,通常以百分比形式表示,这个比值能够反映出数据集的变异程度,即数据点相对于平均值的偏离程度,RSD的计算公式如下:
RSD = (SD / Mean) × 100%
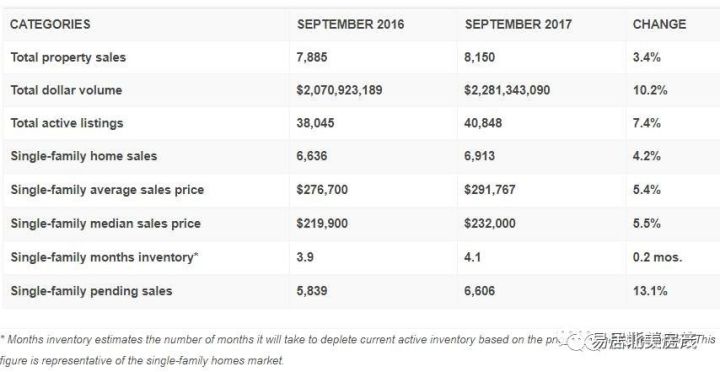
SD表示标准偏差,Mean表示数据平均值,标准偏差是各数值与平均值之差的平方和的平均值的平方根,用于衡量数据集的离散程度,而RSD则是将标准偏差与平均值相结合,以百分比形式表示数据集的变异程度。
RSD的计算方法
RSD的计算过程相对简单,但需要注意一些细节,我们需要计算数据集的平均值和标准偏差,平均值是所有数值的总和除以数值的数量,而标准偏差则是各数值与平均值之差的平方和的平均值的平方根,我们将标准偏差除以平均值,并乘以100%,得到RSD的值。
在实际应用中,我们可以使用各种统计软件或编程语言来计算RSD,在Excel中,我们可以使用AVERAGE函数计算平均值,使用STDEV函数计算标准偏差,然后将两者相除并乘以100%得到RSD的值,许多统计软件也提供了直接计算RSD的功能,使得计算过程更加便捷。
RSD的应用场景
RSD在多个领域都有广泛的应用,特别是在需要评估测量精密度和数据可靠性的场景中,以下是一些典型的应用场景:
1、实验室分析:在化学、生物、物理等实验室中,研究人员经常需要对样品进行多次测量以获取准确的结果,RSD可以用于评估这些测量结果的精密度,即各次测量值之间的离散程度,较小的RSD值表明测量结果的精密度较高,反之则表明精密度较低。
2、质量控制:在制造业中,质量控制是确保产品符合规格和要求的关键环节,RSD可以用于评估生产过程中的变异程度,从而判断产品质量是否稳定,较大的RSD值可能意味着生产过程中存在较大的变异,需要采取措施进行改进。
3、医学研究:在医学研究中,研究人员经常需要收集大量的临床数据以评估治疗方法的有效性和安全性,RSD可以用于评估这些数据集的变异程度,从而判断研究结果的可靠性和稳定性,较小的RSD值表明研究结果较为一致和可靠,反之则可能存在较大的误差和不确定性。
4、金融市场分析:在金融市场分析中,RSD可以用于评估股票价格、汇率等金融指标的波动程度,较大的RSD值可能意味着市场存在较大的不确定性和风险,需要谨慎投资;而较小的RSD值则可能表明市场相对稳定和可预测。
RSD在数据分析中的重要作用
RSD在数据分析中扮演着至关重要的角色,它为我们提供了一种量化数据离散程度的方法,使得我们能够更加准确地了解数据集的变异程度和分布情况,RSD可以帮助我们评估测量结果的精密度和可靠性,从而判断数据是否可用于进一步的分析和决策,RSD还可以用于比较不同数据集之间的变异程度,从而揭示它们之间的相似性和差异性。
需要注意的是,RSD并不是万能的,在某些情况下,它可能无法完全反映数据的真实情况,当数据集中存在极端值时,RSD可能会受到较大的影响而失真,在使用RSD进行数据分析时,我们需要结合其他统计指标和实际情况进行综合判断。
RSD是一个重要的统计指标,用于描述数据集中各数值相对于其平均值的离散程度,它在多个领域都有广泛的应用,特别是在需要评估测量精密度和数据可靠性的场景中,通过计算RSD并结合其他统计指标和实际情况进行综合判断,我们可以更加准确地了解数据集的变异程度和分布情况,为科学研究和数据分析提供有力的支持。








发表评论