探索数学奥秘:什么是质数与合数
在数学的广袤领域中,质数和合数是两个至关重要的概念,它们不仅在数学理论研究中占据重要地位,更在实际应用中发挥着不可替代的作用,究竟什么是质数和合数呢?本文将带领大家一同探索这两个概念的奥秘。
我们来了解质数的定义,质数,又称素数,是指在大于1的自然数中,除了1和它本身以外不再有其他因数的数,换句话说,质数只有两个正因数:1和它本身,2、3、5、7等都是质数,质数在数学中具有独特的地位,它们不仅是数学研究的基础,还是密码学、计算机科学等领域的重要工具,在密码学中,质数被广泛应用于公钥加密系统,保障了信息安全。
我们探讨合数的概念,与质数相反,合数是指在大于1的自然数中,除了1和它本身以外还有其他因数的数,换句话说,合数至少有三个正因数,4、6、8、9等都是合数,合数在数学中同样具有广泛的应用,它们与质数共同构成了自然数的完整体系,在解决实际问题时,合数也发挥着重要作用,在统计学中,合数可以用于描述数据的分布特征;在物理学中,合数可以用于描述物体的运动状态等。
了解了质数和合数的定义后,我们还需要掌握它们之间的关系,质数和合数是互斥的,即一个数要么是质数,要么是合数(除了1以外,1既不是质数也不是合数),质数是构成合数的基础,任何一个合数都可以分解为若干个质数的乘积,这一性质被称为质因数分解,质因数分解在数学中具有广泛的应用,它可以帮助我们简化复杂的数学问题,揭示数学现象的本质。
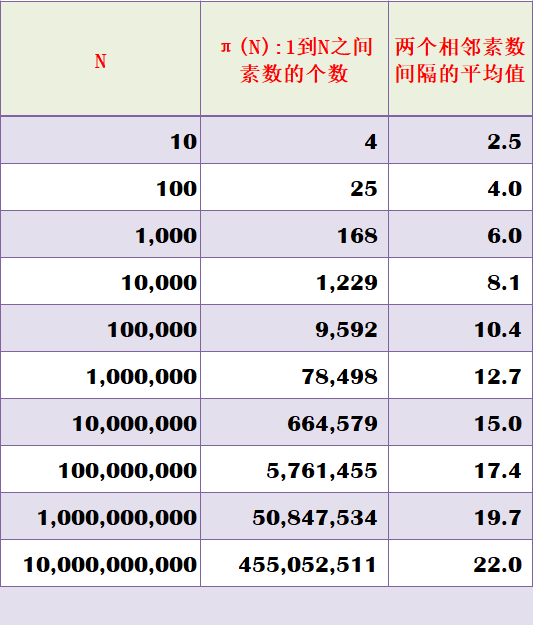
质数和合数在数论、代数、几何等领域都有着广泛的应用,在数论中,质数和合数的性质被深入研究,为数学理论的发展提供了有力支持;在代数中,质数和合数被用于构建各种代数结构,如群、环、域等;在几何中,质数和合数可以用于描述图形的性质,如多边形的边数、图形的对称性等。
值得一提的是,质数和合数的研究不仅局限于数学领域,它们还与其他学科产生了紧密的交叉,在物理学中,质数和合数与量子力学、粒子物理等领域的研究密切相关;在化学中,质数和合数与分子结构、化学反应等问题的研究紧密相连;在生物学中,质数和合数与遗传密码、生物信息学等领域的研究也密不可分。
质数和合数是数学中两个重要的概念,它们不仅在数学理论研究中占据重要地位,更在实际应用中发挥着不可替代的作用,通过深入了解质数和合数的定义、性质及应用,我们可以更好地掌握数学的本质,拓展数学的应用领域,为人类的科技进步和社会发展贡献力量,在未来的研究中,我们期待质数和合数能够继续发挥重要作用,引领数学及其他学科的发展迈向新的高度。









发表评论